1. Using R's C API

Creating C functions that are callable from R
Calling expSmooth from R
Creating R objects within C code
References

The purpose of this section is explaining how to interface R with C/C++ using the raw C API provided by R. In practice it is generally preferable to use the Rcpp package to interface R with C++, but it is useful to know how R’s C API works to have an idea of what is going on under the hood when you use Rcpp. Besides, many of the functions in base R are written in C using the R’s C API and do not use Rcpp. This section assumes that you have some basic knowledge of C.

Creating C functions that are callable from R

To provide some motivation, consider the following data:

library(gamair)
library(tibble)
data(chicago)
chicago <- as_tibble(chicago)
chicago

## # A tibble: 5,114 × 7
##    death pm10median pm25median o3median so2median   time  tmpd
##    <int>      <dbl>      <dbl>    <dbl>     <dbl>  <dbl> <dbl>
##  1   130     -7.43          NA    -19.6     1.93  -2556.  31.5
##  2   150     NA             NA    -19.0    -0.986 -2556.  33  
##  3   101     -0.827         NA    -20.2    -1.89  -2554.  33  
##  4   135      5.57          NA    -19.7     6.14  -2554.  29  
##  5   126     NA             NA    -19.2     2.28  -2552.  32  
##  6   130      6.57          NA    -17.6     9.86  -2552.  40  
##  7   129     -0.434         NA    -15.4    -5.82  -2550.  34.5
##  8   109     -5.43          NA    -12.2    -5.11  -2550.  29  
##  9   125     -0.571         NA    -20.1     0.182 -2548.  26.5
## 10   153     NA             NA    -18.6    -2.05  -2548.  32.5
## # … with 5,104 more rows

The chicago data set contains data on daily air pollution and death rate for Chicago (see ?chicago for details). Given this data, one might be interested in analysing the relation between the number of deaths and air pollution. In particular, one could consider the following GAM model (taken from Wood, 2017, page 347) \[ \text{death}_t \sim \text{Poi}(\lambda_t), \] \[ \log \lambda_t = f_1(\text{time}_t) + f_2(\text{pm10}_t) + f_3(\text{so2}_t) + f_4(\text{o3}_t) + f_5(\text{tmpd}_t), \] Which can be fitted using mgcv as follows:

library(mgcViz)
fit0 <- bam(death ~ s(time, k = 200) + s(pm10median) + s(so2median) + s(o3median) +
                    s(tmpd),
            data = chicago, family = poisson, discrete = TRUE)

Then we can use mgcViz to plot the effect of the three pollutants and of the daily temperature:

fit0 <- getViz(fit0)
print(plot(fit0, select = 2:5), pages = 1)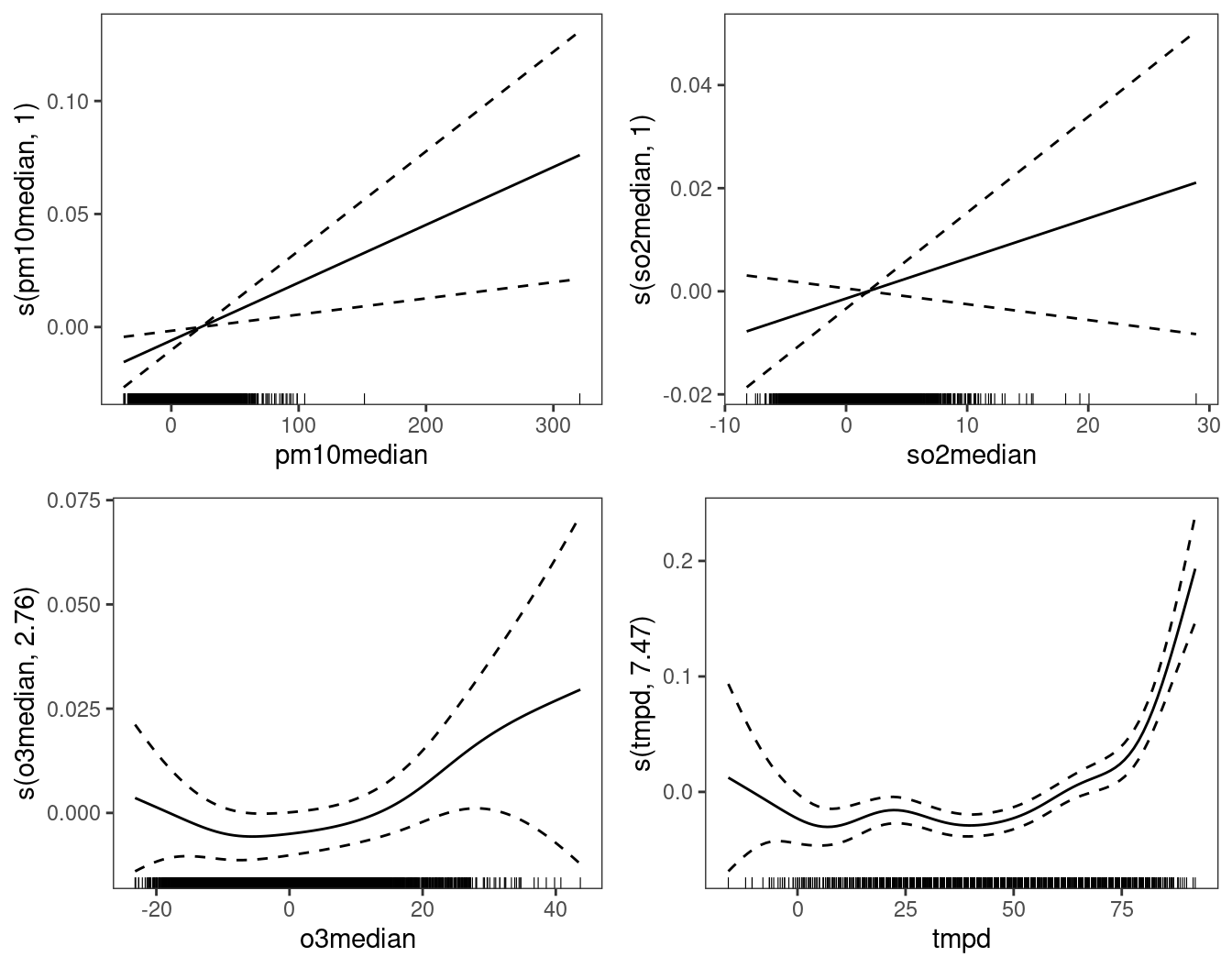

The effect of so2 doesn’t seem to be important, hence it might make sense to remove it from the model. Another thing that we could try, is to check whether the number of deaths depends on the temperatures (tmpd) registered in the last few days, rather than only on the temperature on the same day. Rather than simply using lagged values of the temperature, we could consider building a new variable obtained by exponentially smoothing the temperature, that is \[ \text{tmpdSmooth}_t = \alpha \, \text{tmpdSmooth}_{t-1} + (1 - \alpha) \, \text{tmpd}_t, \] with $\alpha \in (0, 1)$.

Now, assume that we want to implement a function, say, expSmooth to calculate the exponential smooth of a variable in C, and that we want to be able to call it from R. The C code for such a function is:

#include <R.h>
#include <Rinternals.h>

SEXP expSmooth(SEXP y, SEXP ys, SEXP n, SEXP a)
{
  int ni;
  double *xy, *xys;
  double ai;
  
  xy = REAL(y); 
  xys = REAL(ys);
  ni = INTEGER(n)[0];
  ai = REAL(a)[0];

  xys[0] = xy[0];
  for(int i = 1; i < ni; i++){
    xys[i] = ai * xys[i-1] + (1 - ai) * xy[i];
  }
  
  return R_NilValue;
}

Before explaining how expSmooth can be called from R, let’s try to break it down. The first two lines are there to include two header files that contain some R-related C functions and macros. For example REAL is defined in Rinternals.h as can be verified by looking at the source code by doing (not shown here):

rinternals <- file.path(R.home("include"), "Rinternals.h")
file.show(rinternals)

The expSmooth function returns an SEXP, which is also the class of its inputs. A object of class SEXP is a pointer to an S expression, that is a pointer to an object in the R environment. Hence, importantly, the inputs are passed to expSmooth by reference and are not copied. Here our inputs are:

y, the vector to be smoothed;
ys, the vector which will contain the smoothed version of y;
n, a scalar indicating the length of y and ys;
a, the $\alpha$ coefficient.

Even though all the arguments of expSmooth are of class SEXP, it is important to know that SEXP is a variant type, that is a C object whose subtype is known only at runtime, with subtypes that cover all data structures in R. Examples of subtypes are:

REALSXP a numeric vector such as c(1.2, 0.45);
LGLSXP a logical vector such as c(TRUE, FALSE, FALSE);
INTSXP an integer vector such as c(2L, 34L, 1L);
VECSXP a list such as list("a" = 2, "b" = c(5, 4)).

See the R internal documentation for a complete list.

The first lines of the function’s body are:

int ni;
double *xy, *xys;
double ai;

where we are creating four C objects, which are initialized using:

xy = REAL(y); 
xys = REAL(ys);
ni = INTEGER(n)[0];
ai = REAL(a)[0];

We are using the macro function REAL to access object y. In particular, REAL returns a double pointer to the real part of the SEXP y. Similarly, INTEGER(n) returns a pointer to the integer part of n and by doing [0] we are extracting the value of its first element. Hence, here there is the assumption that the subtype of y is REALSXP and that the subtype of n is INTSXP. Otherwise if, for example, n was a real vector of type REALSXP, calling INTEGER would trigger an error at runtime, as we shall see.

The computation actually happens here:

xys[0] = xy[0];
for(int i = 1; i < ni; i++){
  xys[i] = ai * xys[i-1] + (1 - ai) * xy[i];
}

In the first line we are initializing by setting $\text{tmpdSmooth}_1 = \text{tmpd}_1$, than the rest is straighforward C code. Notice that the function returns:

return R_NilValue;

where R_NilValue is defined in Rinternals.h and it’s the C equivalent of R’s NULL. Hence the function is not returning anything useful, but the smoothed variable is obtained by modifying the xys vector in place (that is, without making a copy).

Calling expSmooth from R

Now, assume that expSmooth is contained in a file called expSmooth.c, which in our case can be found in our working directory, as you could see from the following call to the command line (the output is hidden here):

system("ls *.c")

Here we will explain how to call expSmooth using the .Call interface in R. .Call can be used to call C functions that accept variables of class SEXP as inputs and return an object of class SEXP. Indeed, we created the expSmooth function with this requirement in mind.

The first thing that we need to do is to compile the C code as follows

system("R CMD SHLIB expSmooth.c")

This will create two files, expSmooth.o and expSmooth.so, containing binary code. The .so object is a shared object which can be loaded in R by doing:

dyn.load("expSmooth.so")

Having done this, the expSmooth function is now available at R level:

is.loaded("expSmooth")

## [1] TRUE

See the Creating shared objects section of the Writing R Extensions manual for more details on how this works.

Having loaded expSmooth in R, we can now call it using .Call:

nch <- nrow( chicago )
tmpSmooth <- numeric(nch)

.Call("expSmooth", chicago$tmpd, tmpSmooth, nch, 0.8)

## NULL

As expected the function returns NULL, but the smoothed temperature is now contained in tmpSmooth:

plot(chicago$tmpd[1:1000], col = "grey", ylab = "Temp")
lines(tmpSmooth[1:1000], col = 2)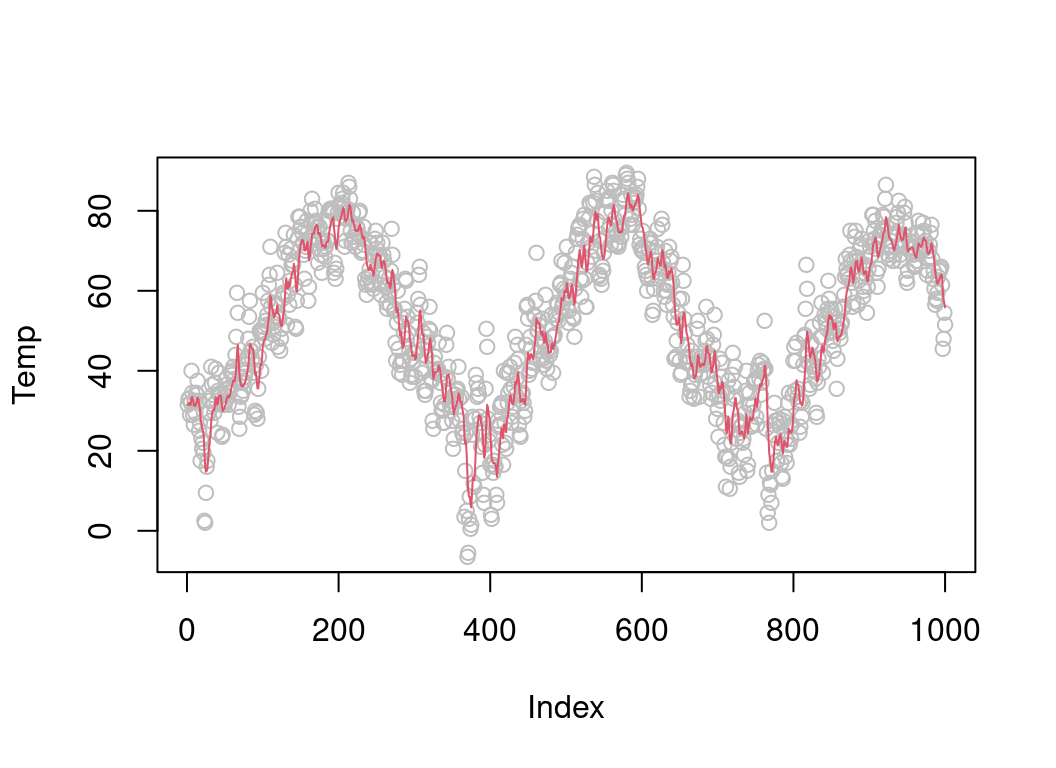

To check whether our function actually works, let’s compare it with an R version of it:

expSmoothR <- function(x, a){

  n <- length(x)
  xs <- x

  for(ii in 2:n){
   xs[ii] <- a * xs[ii - 1] + (1 - a) * x[ii]
  }

  return(xs)

}

The output of the R and C version is identical:

max( abs(tmpSmooth - expSmoothR(chicago$tmpd, 0.8)) )

## [1] 0

Having verified that our C function for exponential smoothing does the right thing, let’s see how it compares with its R version in terms of computing time:

smoR <- function() expSmoothR(chicago$tmpd, 0.8)
smoC <- function() .Call("expSmooth", chicago$tmpd, tmpSmooth, nch, 0.8)

library(microbenchmark)
microbenchmark(smoR(), smoC(), times = 500)

## Unit: microseconds
##    expr   min    lq     mean median    uq    max neval
##  smoR() 582.9 585.5 592.1336  587.2 590.6 1970.0   500
##  smoC()  18.9  19.1  21.9564   19.1  19.3 1330.7   500

So the C version is more than 10 times faster. The comparison it somewhat unfair, because the R function is allocating memory containing the smoothed temperature at every call, while the C version is re-using the memory allocated to the tmpSmooth vector. However, the ability to overwrite R objects without copying them is one of the reasons for interfacing R with C.

We now go back to our original application, and fit a model which excludes so2 which didn’t seem to matter and that includes the effect of smoothed temperature:

chicago$tmpSmooth <- tmpSmooth
fit1 <- bam(death ~ s(time, k = 200) + s(pm10median) + s(o3median) +
                    s(tmpd) + s(tmpSmooth),
                   data = chicago, family = poisson, discrete = TRUE)

We now plot the effects of the two temperature effects:

fit1 <- getViz(fit1)
print(plot(fit1, select = 4:5), pages = 1)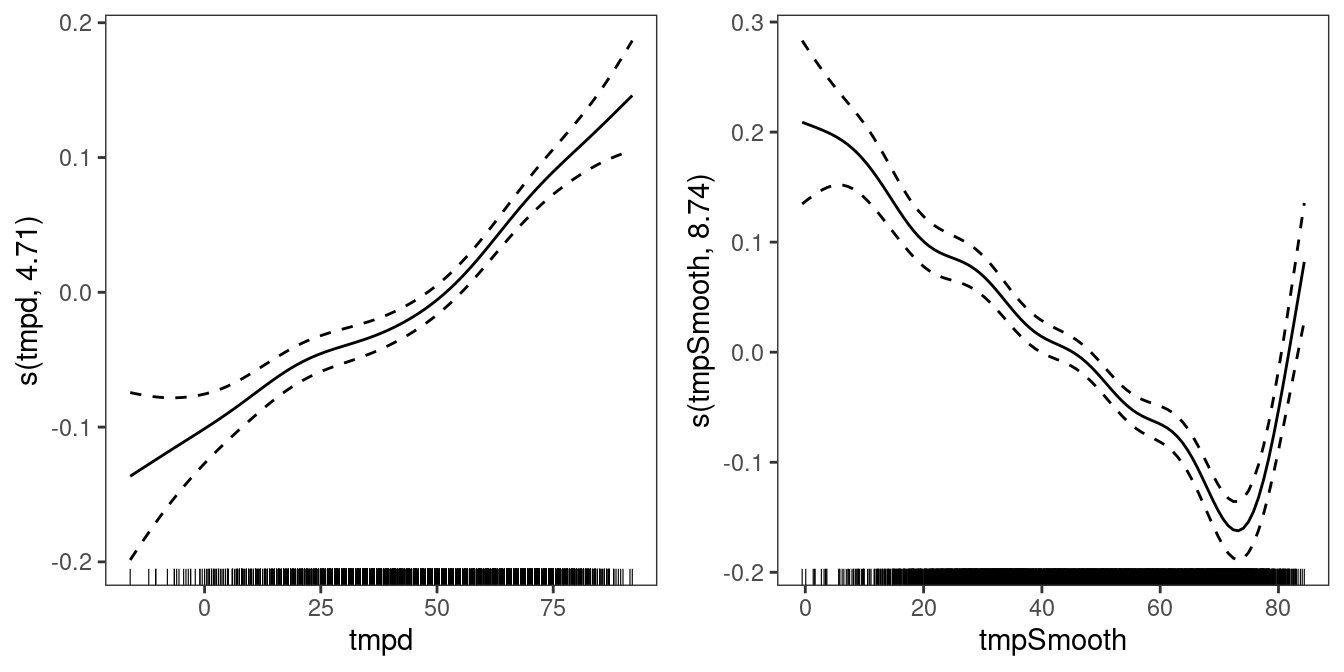

The plots shows that the effect of smoothed temperature is quite important, and the new model seems to do better than the old model in terms of AIC:

AIC(fit0, fit1)

##            df      AIC
## fit0 145.0587 37889.99
## fit1 141.5415 37862.83

Creating R objects within C code

Here we try to refine the expSmooth function created above. Firstly notice that, while expSmooth does not make any explicit assumption about the subtype of its SEXP input, trying to smooth the number of death leads to:

.Call("expSmooth", chicago$death, tmpSmooth, nch, 0.8)
# Error: REAL() can only be applied to a 'numeric', not a 'integer'

Because xy = REAL(y); triggers an error which signals that y should be a vector of reals, not of integers. To smooth the number of death we must pass as.double(chicago$death). However, expSmooth does not check for other things as well. For example, there nothing guaranteeing that argument n matches the length of the input vectors y and ys. For example, the following code:

.Call("expSmooth", chicago$tmpd, tmpSmooth, nch + 10L, 0.8) # do NOT run this!

might run without any indication that something wrong has happened. But $n$ is 10 units longer than length(chicago$tmpd), which mean that the last 10 iterations of this loop:

for(int i = 1; i < ni; i++){
  xys[i] = ai * xys[i-1] + (1 - ai) * xy[i];
}

are reading outside the memory allocated to xy and writing outside the memory allocated to xys. This is a serious problem, and our current version of expSmooth is entirely relying on the assumption that the user will call it with the right arguments.

A safer version of expSmooth might be something like this:

#include <R.h>
#include <Rinternals.h>

SEXP expSmooth2(SEXP y, SEXP a)
{
  int ni;
  double *xy, *xys;
  double ai;
  SEXP ys;
  
  y = PROTECT(coerceVector(y, REALSXP));
  ni = length(y);
  ys = PROTECT(allocVector(REALSXP, ni));
  
  ai = REAL(a)[0];
  xy = REAL(y); 
  xys = REAL(ys);
  
  xys[0] = xy[0];
  for(int i = 1; i < ni; i++){
    xys[i] = ai * xys[i-1] + (1 - ai) * xy[i];
  }
  
  UNPROTECT(2);
  
  return ys;
}

Notice that expSmooth2 has only two arguments: the variable to be smoothed y and the smoothing coefficient a. Then here:

y = PROTECT(coerceVector(y, REALSXP));
ni = length(y);

we are using coerceVector to convert y to subtype REALSXP hence this is analogous to doing as.double in R. The output of coerceVector must be protected from R’s garbage collector using PROTECT, otherwise the memory allocated to y might be deallocated before we finished using it. All R objects allocated in C code must be protected, as failing to do so might lead to intermittent crashes and hard to find bugs. See this blog post for more details. The next line just extracts the length of y and stores it in ni, thus removing the need to pass the length of y as an argument.

Then we allocate memory for the smoothed output:

ys = PROTECT(allocVector(REALSXP, ni));

where we are allocating memory for a vector of doubles with ni elements. This also must be protected, because we are allocating an R object (allocVector is defined in Rinternals.h). The main loop is the same, but expSmooth2 ends with:

UNPROTECT(2);
return ys;

where we are unprotecting two objects and then returning ys. It is important to UNPROTECT as many objects as you have protected, and to UNPROTECT just before returning to R. Failing to UNPROTECT will lead to memory leakage, that is to R objects hanging around in memory while not being useful or accessible in any way.

Having created our new C function, which can be found in expSmooth2.c, we compile it and load it:

system("R CMD SHLIB expSmooth2.c")
dyn.load("expSmooth2.so")

We compare its output with that of the R version:

max(abs(.Call("expSmooth2", chicago$tmpd, 0.8) - expSmoothR(chicago$tmpd, 0.8)))

## [1] 0

which shows that it is working correctly. The computing time is also comparable to that of the old C function:

smoR <- function() expSmoothR(chicago$tmpd, 0.8)
smoC <- function() .Call("expSmooth", chicago$tmpd, tmpSmooth, nch, 0.8)
smoC2 <- function() .Call("expSmooth2", chicago$tmpd, 0.8)

library(microbenchmark)
microbenchmark(smoR(), smoC(), smoC2(), times = 500)

## Unit: microseconds
##     expr   min    lq     mean median    uq    max neval
##   smoR() 582.5 585.6 591.8938 587.25 590.9 1672.6   500
##   smoC()  19.7  19.9  23.2574  20.00  20.2 1541.0   500
##  smoC2()  18.9  19.2  21.6634  19.30  19.6 1045.4   500

despite the fact that it is allocating memory for the output vector at every call. Importantly, expSmooth2 is safer and works directly with integer input vectors:

plot(chicago$death[1:1000], col = "grey")
lines(.Call("expSmooth2", chicago$death, 0.8)[1:1000], col = 2)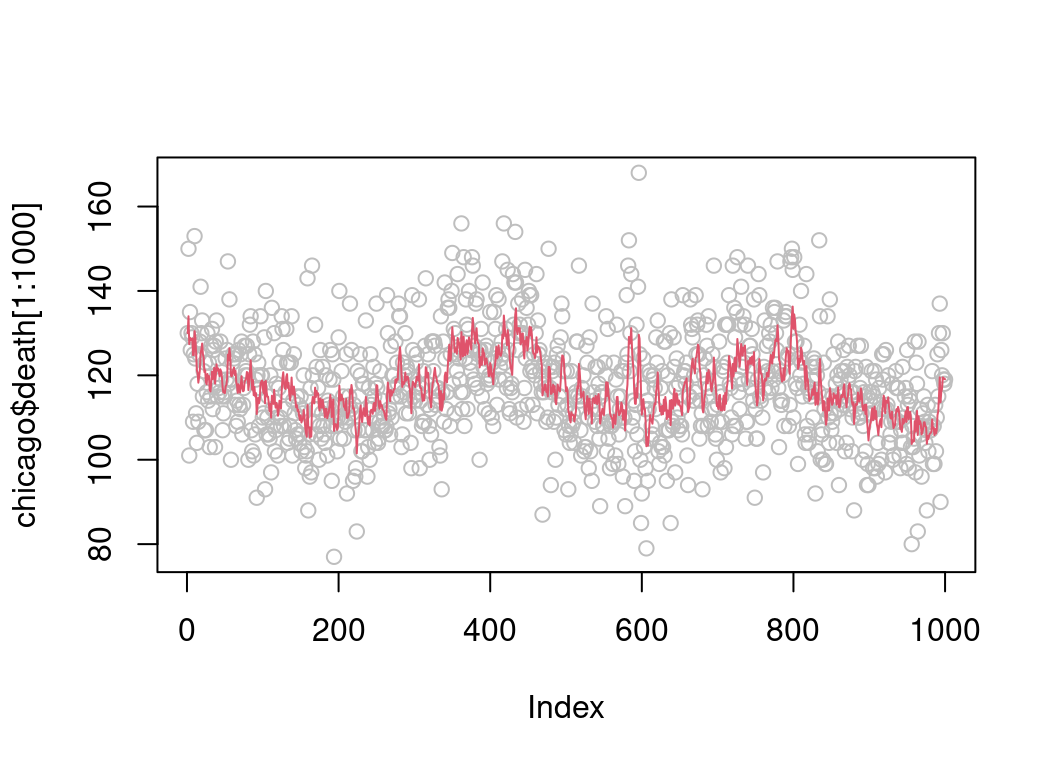

References

Chambers, J.M., 2017. Extending R. Chapman and Hall/CRC.
CRAN. R internals, see https://cran.r-project.org/doc/manuals/r-release/R-ints.html
CRAN. Writing R extensions, see https://cran.r-project.org/doc/manuals/R-exts.html
Wickham H.. R’s C interface, see http://adv-r.had.co.nz/C-interface.html
Wickham H.. R internals, see https://github.com/hadley/r-internals