SC2

Statistical Computing 2

1. Using OpenMP in Rcpp

Here we describe some basic examples on the use of OpenMP to parallelise Rcpp code. We assume that the reader has some basic familiarity with OpenMP. If you need a refresher, have a look at these notes from Chris Wood.

Basic examples

The following Rcpp program simply pauses the system for sec seconds:

library(Rcpp)
sourceCpp(code = '
#include <unistd.h>
#include <Rcpp.h>

// [[Rcpp::export(wait_a_second)]]
bool wait_a_second(int sec)
{
 for(int ii = 0; ii < sec; ii++)
 { 
  sleep(1);
 }
 return 1;
}
')

system.time( wait_a_second(2) )[3]
## elapsed 
##       2

Where sleep is defined in unistd.h. The following function uses OpenMP to wait sec seconds on ncores in parallel:

sourceCpp(code = '
#include <unistd.h>
#include <Rcpp.h>

// [[Rcpp::plugins(openmp)]]

// [[Rcpp::export(wait_a_second_omp)]]
bool wait_a_second_omp(int sec, int ncores)
{

 #if defined(_OPENMP)
  #pragma omp parallel num_threads(ncores)
  #pragma omp for
 #endif
 for(int ii = 0; ii < sec; ii++)
 { 
  sleep(1);
 }
 
 return 1;

 }
')

Note that we used the Rcpp::plugins attribute to include OpenMP in the compilation of the Rcpp function. The key OpenMP directives are

#pragma omp parallel num_threads(ncores)

which indicates the beginning of a parallel section, to be executed on ncores parallel threads, and

#pragma omp for

which tells the compiler that the for loop can be run in parallel. Let try if this works:

system.time(wait_a_second_omp(4, 1))[3]
## elapsed 
##       4
system.time(wait_a_second_omp(4, 4))[3]
## elapsed 
##   1.004
system.time(wait_a_second_omp(16, 16))[3]
## elapsed 
##   1.002

It seems so! Note that the speed up is linear in the number of threads in this case, because each thread is essentially doing nothing. That is, there is no competition for computing resources (i.e., floating-point processing units). To illustrate that this is generally not the case, let us consider the following Rcpp function:

sourceCpp(code = '
#include <Rcpp.h>
using namespace Rcpp;

// [[Rcpp::export(allFiniteSeq)]]
bool allFiniteCpp(NumericVector x)
{

 size_t n = x.size();
 double out = 0;
 
 for(size_t ii = 0; ii < n; ii++)
 {
  out += x[ii];
 }
 
 return R_FINITE(out);

 }
')

which returns TRUE is all the elements of x are finite, FALSE otherwise. We can use OpenMP to parallelise it as follows:

sourceCpp(code = '
#include <Rcpp.h>
#include <omp.h>
using namespace Rcpp;

// [[Rcpp::plugins(openmp)]]

// [[Rcpp::export(allFiniteOMP)]]
bool allFiniteOMP(NumericVector x, int ncores)
{
 size_t n = x.size();
 double out = 0;
 NumericVector z(ncores);
 
 #pragma omp parallel num_threads(ncores)
 {
  int kk = omp_get_thread_num();
  
  #pragma omp for schedule(static)
  for(size_t ii = 0; ii < n; ii++)
  {
   z[kk] += x[ii];
  }
 }
 
 out = sum(z);
 
 return R_FINITE(out);

 }
')

Note that this code:

#pragma omp parallel num_threads(ncores)

marks the beginning of a parallel section of the code, hence the variables declared in this section (e.g, kk) are private to each parallel thread. This code:

int kk = omp_get_thread_num();

retrieves the ID number of each thread (omp_get_thread_num() is defined in omp.h). The rest of the code should be relatively clear.

On my Intel i7-3820 3.60GHz CPU with 4 cores 8 threads I get the following timing:

x <- rnorm(1e7)

library(microbenchmark)
options(microbenchmark.unit="relative")
microbenchmark(all(is.finite(x)),
               allFiniteSeq(x),
               allFiniteOMP(x, 1), 
               allFiniteOMP(x, 4),
               allFiniteOMP(x, 8), 
               allFiniteOMP(x, 16))
Unit: relative
                expr       min        lq       mean    median         uq      max neval
   all(is.finite(x)) 18.892823 17.973095 14.2843653 17.272120 13.0616667 7.876008   100
     allFiniteSeq(x)  4.477392  4.282347  3.2067998  4.076221  2.5890351 1.903284   100
  allFiniteOMP(x, 1)  4.486162  4.288818  3.2039762  4.082022  2.5897148 1.997958   100
  allFiniteOMP(x, 4)  1.198740  1.238068  0.9849882  1.197137  0.7789038 1.127209   100
  allFiniteOMP(x, 8)  1.000000  1.000000  1.0000000  1.000000  1.0000000 1.000000   100
 allFiniteOMP(x, 16)  1.045107  1.103636  1.0457466  1.165450  1.0583197 1.170184   100

Note that the Rcpp version is around 4 times faster that the R code, and that with 4 threads we get roughly a linear speed-up. However, the speed-up gains are negligible after that, and using 16 threads is actually detrimental. This is because a processor with 4 physical cores has probably 4 floating-point (FLOP) units, hence trying to parallelise numerical computations on more than 4 threads does not make sense (the threads will start to compete for the same FLOP units).

One important thing to point out is that R’s C API and the Rcpp API are not thread-safe in generally. Hence, doing things such as:

#pragma omp parallel
{
 NumericVector x(10);
 int u = x.length();
}

is not safe and might behave unexpectedly. In our code for the allFiniteOMP function, above, we do z[kk] += x[ii];, which selects elements of the NumericVector x in parallel. This is not guaranteed to be thread-safe, hence it is preferable to use the thread-safe data structures provided by the RcppParallel R package, which will be discussed later in these notes. In the following section we show how to perform parallel random number generation using OpenMP and a thread-safe RNG.

Parallel random number generation using OpenMP

As other parts of R’s C API, R’s RNG is not thread safe. Hence, Rcpp code such as:

#pragma omp parallel
{
x = R::rbeta(a, b);
}

will produce invalid results and might crash your R session. So, we must adopt a thread-safe RNG, such as the one provided by the sitmo R package.

Before explaining how to use sitmo in parallel, let us consider the following sequential function:

sourceCpp(code = '
#include <Rcpp.h>
#include <sitmo.h>

// [[Rcpp::depends(sitmo)]]

// [[Rcpp::export(sumunif_sitmo)]]
Rcpp::NumericVector sumunif_sitmo(unsigned int n,
                                  unsigned int nstep,
                                  double seed) {
  Rcpp::NumericVector out(n);

  uint32_t coreseed = static_cast<uint32_t>(seed);
  sitmo::prng eng(coreseed);
  
  double mx = sitmo::prng::max();
  double tmp = 0;

   for(unsigned int ii = 0; ii < n; ++ii) {
     tmp = 0.0;
     for(unsigned int kk = 0; kk < nstep; ++kk){
      tmp += eng() / mx;
     }
     out[ii] = tmp;
   }
    
  return out;
}
')

This function simply simulates n sums of nstep uniform U(0, 1) random variables. Hence, it is equivalent to the following R code:

rowSums(matrix(runif(n*nstep), n, nstep))

Let us examine the key steps in runif_sitmo_omp:

Let’s try it:

n <- 1e3
nstep <- 1000

par(mfrow = c(1, 2))
hist(rowSums(matrix(runif(n*nstep), n, nstep)), main = "R", xlab = "x")
hist(sumunif_sitmo(n, nstep = nstep, seed = 1), main = "Sitmo", xlab = "x")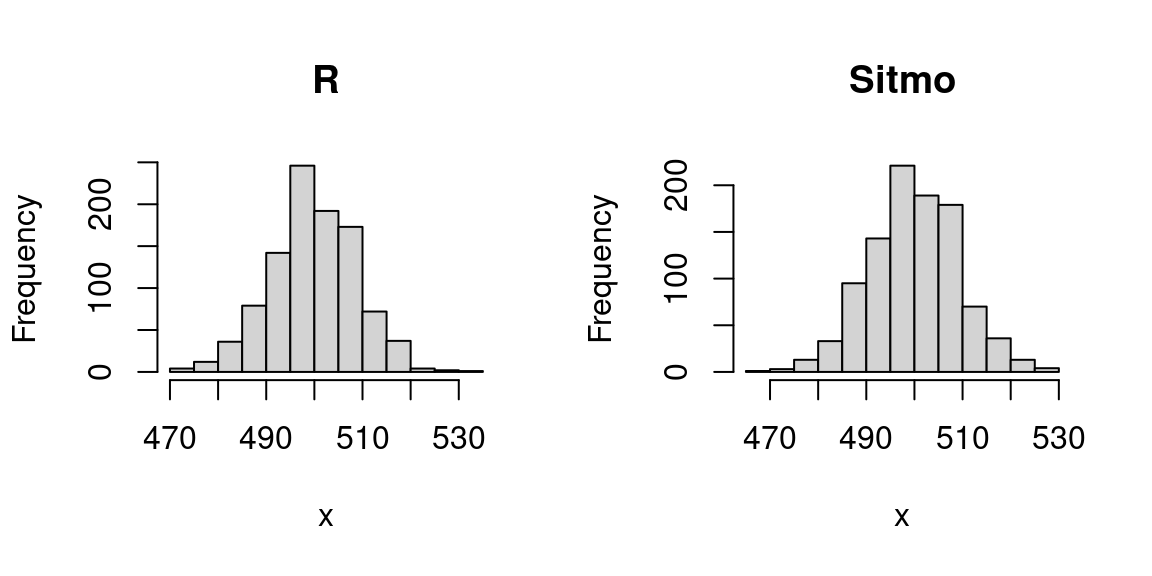

The histograms show the Central Limit Theorem kicking in.

Now, let us look at a parallel version:

sourceCpp(code = '
#include <Rcpp.h>
#include <sitmo.h>

#ifdef _OPENMP
#include <omp.h>
#endif

// [[Rcpp::depends(sitmo)]]
// [[Rcpp::plugins(openmp)]]

// [[Rcpp::export(sumunif_sitmo_omp)]]
Rcpp::NumericVector sumunif_sitmo_omp(unsigned int n,
                                      unsigned int nstep,
                                      Rcpp::NumericVector seeds) {
  Rcpp::NumericVector out(n);
  
  unsigned int ncores = seeds.size();
  
  #ifdef _OPENMP
  #pragma omp parallel num_threads(ncores)
  {
  #endif
  
   uint32_t coreseed = static_cast<uint32_t>(seeds[0]);
   
   #ifdef _OPENMP
    coreseed = static_cast<uint32_t>(seeds[omp_get_thread_num()]);
   #endif
   
   sitmo::prng eng(coreseed);
   
   double mx = sitmo::prng::max();
   double tmp = 0;
  
   #ifdef _OPENMP
    #pragma omp for 
   #endif
   for(unsigned int ii = 0; ii < n; ++ii) {
     tmp = 0.0;
     for(unsigned int kk = 0; kk < nstep; ++kk){
      tmp += eng() / mx;
     }
     out[ii] = tmp;
   }
    
  #ifdef _OPENMP
  }
  #endif
  
  return out;
}
')

Let us test the parallel version:

par(mfrow = c(1, 2))
hist(rowSums(matrix(runif(n*nstep), n, nstep)), main = "R", xlab = "x")
hist(sumunif_sitmo_omp(n, nstep = nstep, seed = 1:4), main = "Sitmo", xlab = "x")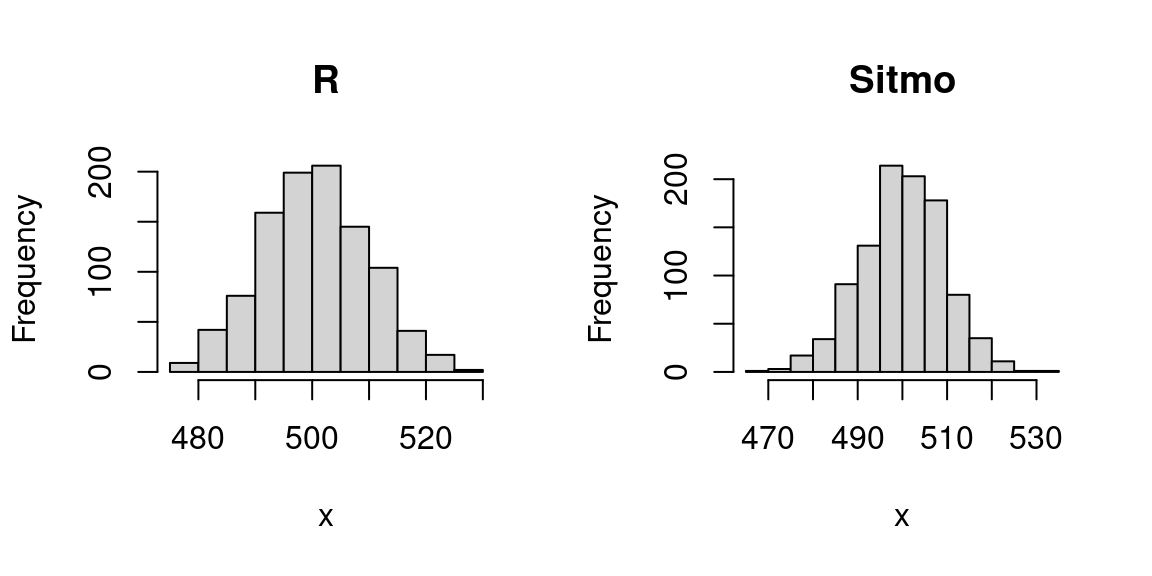

It seems to work fine. Let’s look at the CPU time:

microbenchmark(R = rowSums(matrix(runif(n*nstep), n, nstep)),
               sitmo = sumunif_sitmo(n, nstep = nstep, seed = 1),
               sitmo_omp1 = sumunif_sitmo_omp(n, nstep = nstep, seeds = 1),
               sitmo_omp4 = sumunif_sitmo_omp(n, nstep = nstep, seeds = 1:4), 
               sitmo_omp16 = sumunif_sitmo_omp(n, nstep = nstep, seeds = 1:16), 
               times = 100
               )

On the system described above, I get:

Unit: relative
        expr       min        lq      mean    median        uq       max neval
           R 19.129317 18.220434 15.896634 16.341999 15.275812 22.446736   100
       sitmo  4.895919  4.664486  3.910135  4.147784  3.596815  2.421466   100
  sitmo_omp1  4.887580  4.652173  3.924101  4.135457  3.600384  2.472559   100
  sitmo_omp4  1.231661  1.769258  1.467673  1.584121  1.359834  1.210142   100
 sitmo_omp16  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000   100

Hence, Rcpp is four times faster than R, and we get an acceleration of factor of a little bit more than 2 by using 4 cores. The acceleration levels off if we use more than 4 threads, but in this case we seem to be able to get some extra speed gains by using more threads than actual physical cores. It is difficult to know why this is the case.

References